
It is indicated altitude corrected for non-standard temperature and pressure. True altitude is the actual elevation above mean sea level. Also referred to as radar height or feet/meters above ground level (AGL). It can be measured using a radar altimeter (or absolute altimeter). In UK aviation radiotelephony usage, the vertical distance of a level, a point or an object considered as a point, measured from mean sea level this is referred to over the radio as altitude.Ībsolute altitude is the vertical distance of the aircraft above the terrain over which it is flying. Indicated altitude is the reading on the altimeter when it is set to the local barometric pressure at mean sea level. There are several types of altitude in aviation: When flying at a flight level, the altimeter is always set to standard pressure (29.92 inHg or 1013.25 hPa). Pressure altitude divided by 100 feet (30 m) is the flight level, and is used above the transition altitude (18,000 feet (5,500 m) in the US, but may be as low as 3,000 feet (910 m) in other jurisdictions) so when the altimeter reads 18,000 ft on the standard pressure setting the aircraft is said to be at Flight level 180. On the flight deck, the definitive instrument for measuring altitude is the pressure altimeter, which is an aneroid barometer with a front face indicating distance (feet or meters) instead of atmospheric pressure. Aviation altitude is measured using either mean sea level (MSL) or local ground level (above ground level, or AGL) as the reference datum. Parties exchanging altitude information must be clear which definition is being used.
#Altitude geometry def how to
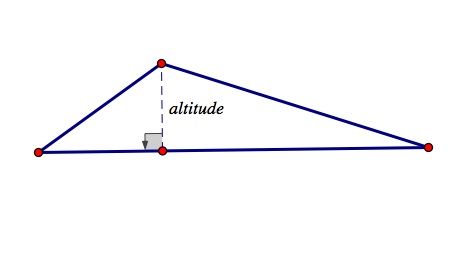
You also know what the Pythagorean Theorem is ( a 2 + b 2 = c 2) and how to prove it, and what the right triangle altitude theorem is (the altitude of a right triangle drawn to the hypotenuse c forms two similar right triangles that are also similar to the original right triangle) and how to prove it.In aviation, the term altitude can have several meanings, and is always qualified by explicitly adding a modifier (like true altitude), or implicitly through the context of the communication. Lesson SummaryĪfter going through the videos, reading the lesson and examining the pictures, you now know how to identify a right triangle (by its interior right angle), what its identifying property is (it has one interior right angle). Since each of the two smaller triangles are similar to the larger triangle, they are similar to each other. Here ∠ B D C = ∠ A C B, and ∠ D B C = ∠ A B C, so again, (by the AA postulate): Go through the figure again, concentrating on the larger, new triangle B C D. This means two angles of △ A D C and △ A B C are similar, making the triangles themselves similar (by the Angle-Angle postulate or AA postulate): You can prove this by seeing that new triangle's ∠ A D C = original triangle's ∠ A C B, while new triangle's ∠ C A D = original triangle's ∠ C A B.

Each of these triangles is similar to the other triangle, and both are similar to the original triangle.
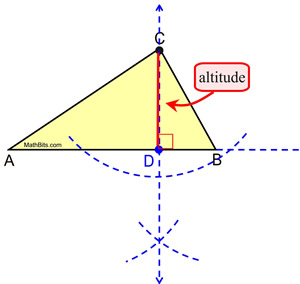
The altitude divided ∠ C, and also created two right angles where it intersected hypotenuse c.Ĭall the point where the altitude h touches hypotenuse c point D. This altitude h creates two smaller triangles inside our original triangle. This puts ∠ A to the bottom left, and ∠ B to the bottom right.Ĭonstruct an altitude (or height) h from the interior right angle C to hypotenuse c (so it is perpendicular to c). The right triangle altitude theorem tells us that the altitude of a right triangle drawn to the hypotenuse c forms two similar right triangles that are also similar to the original right triangle.Ĭonstruct △ A B C so that hypotenuse c is horizontal and opposite right angle C, meaning legs a and b are intersecting above c to form the right angle C. Learn how to use the Pythagorean Theorem to calculate the length of one side of a right triangle. The sides opposite the complementary angles are the triangle's legs and are usually labeled a and b. The other two angles in a right triangle add to 90 ° they are complementary. Opposite it is the triangle's hypotenuse, the longest of the three sides, usually labeled c. We already know the square vertex of the right triangle is a right angle. "Right" refers to the Latin word rectus, meaning "upright." Hypotenuse and Sides of a Right Triangle The term "right" triangle may mislead you to think "left" or "wrong" triangles exist they do not. In drawing right triangles, the interior 90 ° angle is indicated with a little square □ in the vertex. When one of those interior angles measures 90 °, it is a right angle and the triangle is a right triangle. Prove the right triangle altitude theoremĪll triangles have interior angles adding to 180 °.Understand the identifying property of right triangles.After viewing the video, looking over the pictures, and reading the lesson, you will be able to:


 0 kommentar(er)
0 kommentar(er)
