
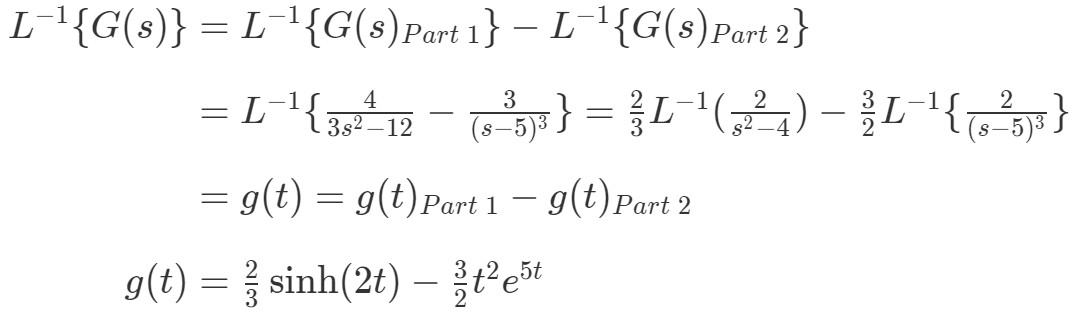
All three kinds of implementations load this file at the first time and use it for inverse Laplace transformation. There is a separate file (iltcme.json) that contains the pre-computed parameters of the CME distributions.
INVERSE LAPLACE TRANSFORM TABLE DOWNLOAD
The implementation of the procedure in Mathematica, Matlab and IPython environments is available to download from this github repository. Miklos Telek: telek (at) hit (dot) bme (dot) hu.Illes Horvath: horvath (dot) illes (dot) antal (at) gmail (dot) com.Gabor Horvath: ghorvath (at) hit (dot) bme (dot) hu.In case of any questions about the method or the implementation do not hesitate to contact us: Probability in the Engineering and Informational Sciences, page 1–17, 2021. Concentrated matrix exponential distributions with real eigenvalues. The parameters of these concentrated ME distributions where determined up to order 31: In the following paper we have published a conjecture that in the class of matrix-exponential distributions the cosine-squared form provides the minimal coefficient of variation. The results leading to the CME-based ILT method have been achieved incrementally. Furthermore, the coefficients can be pre-computed and stored in a file, the complexity of determining them does not make the ILT process slow neither does it make the implementation difficult. However, the resulting \(f_1^n(t)\) (that is the density function of a concentrated matrix-exponential distribution) is always non-negative, and is very steep (a good approximation of the Dirac delta function). In case of the CME approach determining the coefficients is a complex procedure, with a numerical optimization step also involved. In the Euler and the Gaver methods the algorithm to obtain these constants is relatively simple, but the resulting \(f_1^n(t)\) functions can go down to the negative range, too, which can be a source of over- or under-shooting when inverting the Laplace transform. The exact form of this function plays a fundamental role in the Laplace transform inversion, and this is the point where the different ILT methods differ: the Euler, the Gaver and the CME methods provide different \(\eta_k\) coefficients and \(\beta_k\) exponents. According to the Abate-Whitt framework the \(\delta(T-t)\) function is approximated by a weighted sum of exponentials consisting of \(n\) terms, that is Where \(\delta(t)\) is the Dirac delta function. How does it work?Īssume we have a function \(h\).
INVERSE LAPLACE TRANSFORM TABLE FREE
It always results valid probabilities due to the over- and under-shooting free behavior. The CME method is the ideal choice when working with probability distributions. Oscillation gets worse when the order is increasedĬonverges very slowly by increasing the order Gets more accurate when the order is increased Poor approximation around the sharp edges Oscillates around sharp changes of the function Smooth, over- and under-shooting free approximation
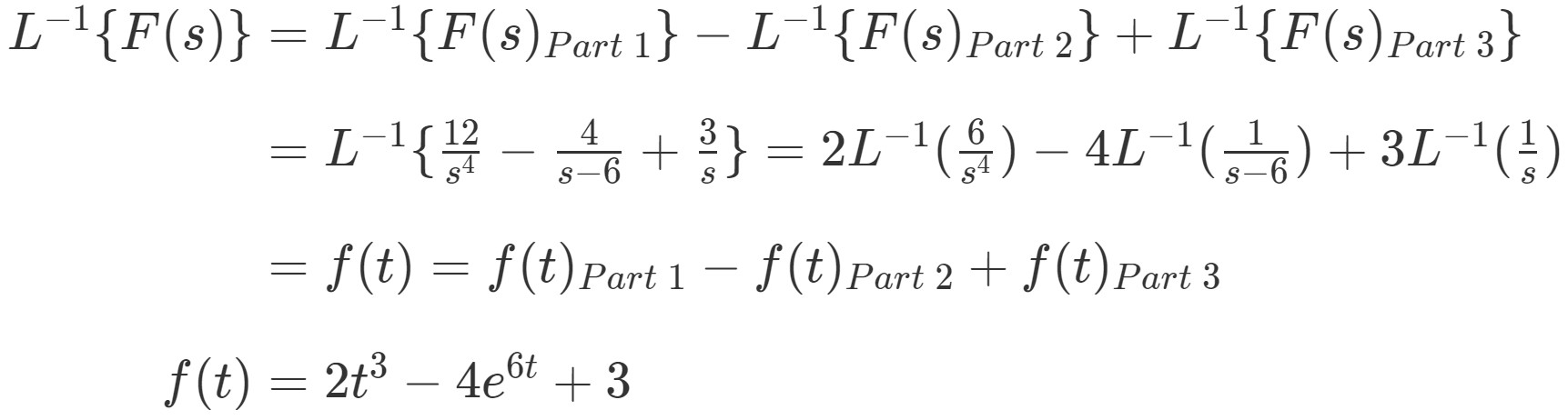
Poor numerical behavior, needs multi-precision arithmetic Our new method, called CME, is far superior to them.Įxcellent numerical stability, even at machine precisionĪcceptable numerical stability up to a given order The Abate-Whitt methods, in particular the Euler and the Gaver method, are very popular and widely used. There is a class of methods, the Abate-Whitt framework, where the Laplace transform is evaluated always at the same points, independent of the form of the Laplace transform.
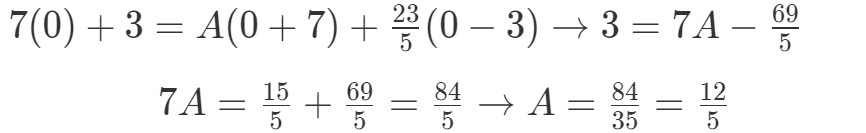
These procedures evaluate the known Laplace transform expression at certain points to approximate the inverse of the Laplace transform at a given point. Usually when performing inverse Laplace transforms, I decompose the function into partial fractions, and then look up standard transforms in a table.There are many inverse Laplace transform procedures published in the scientific literature.


 0 kommentar(er)
0 kommentar(er)
